This is about a perfect loop technique that’s probably the one I use the most. It’s quite abstract and general: the idea is to have queue of objects. During the time of one gif loop, each object will take the position or state of a next one. That’s why I call it the “replacement” technique.

Basically we have a function like this one to draw one object:

p is a continuous parameter, increasing with time.

To draw all objects with a perfect loop we do:

K is the number of objects in the queue, I have often used this notation and I keep it in case you see the source code of my older gifs. Here we divide by K assuming p ranges from 0 to 1 in drawThing but that’s not necessary. This works because t starts at 0 and ends at 1, so you reach the next index with (i+t) at the end of the loop.

If drawThing has same state at p=0 and p=1 there is no problem, but if not you might just make objects out of sight at p=0 and p=1 to avoid objects that appear or disappear suddenly.

So that’s basically everything about this technique but so far it’s quite abstract… let’s take an example.

An example for the replacement technique

The aim is to make an animation like this one:

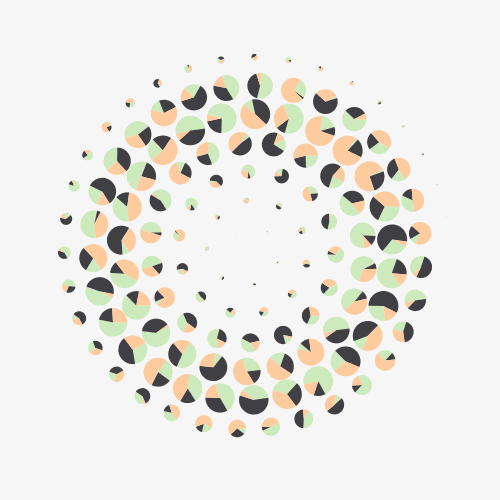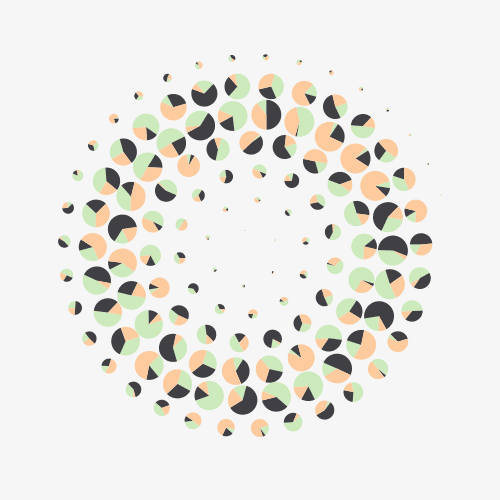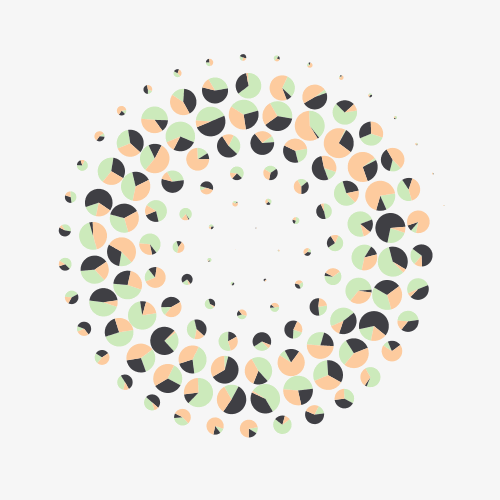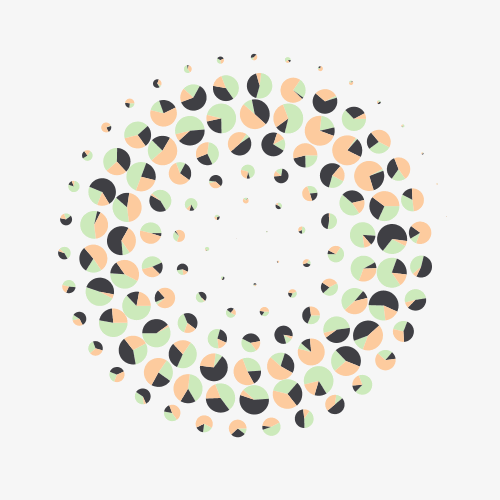
Here K=130 and the drawThing function draws a single pie.

Let’s choose a color palette from colorhunt.co:

To get the position at parameter p on the spiral one can use those equations:

The sqrt(p) gives us a good parametrization with constant speed.

The idea for the pie design is to use three random values with noise. The ratio between a value and the sum of all values gives us the share of angle of a part.

Here is some code to get random values that change with p:

It’s basically 1D noise. The pow function is there to sometimes have values that are much larger than the others.

Here is the code to draw a single pie at p:

Note that some rotation alpha of constant speed is added. The radius r of the pie varies so that pies appear and then disappear (p=0 and p=1).

So now we can use this piece of code in draw() to do the replacement technique:

The entire code is the following:

And here is a reminder of the result:

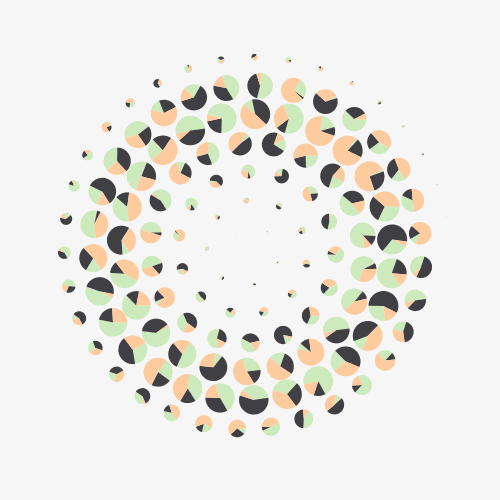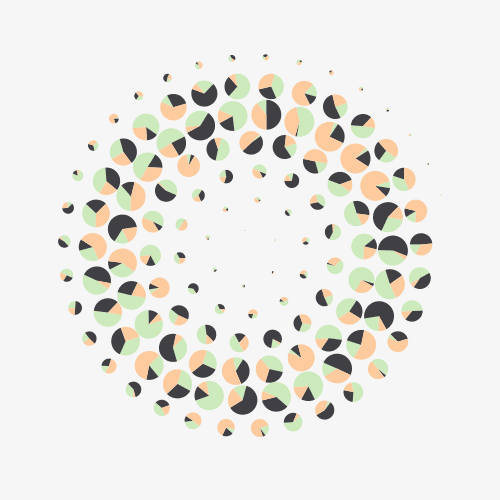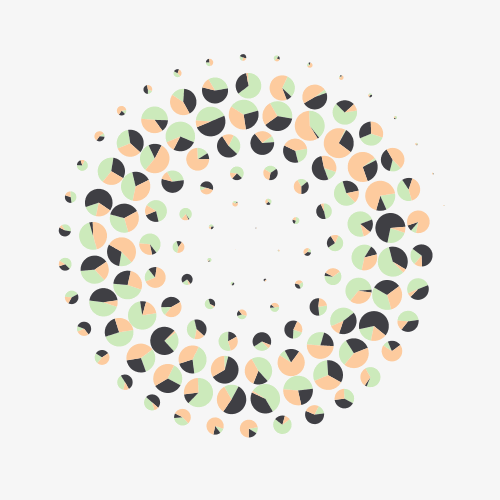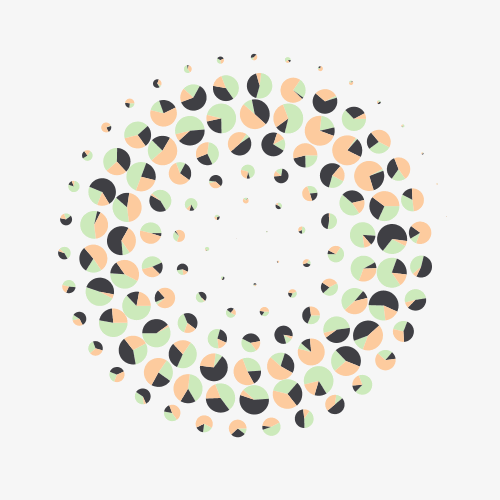
I often use the replacement technique with object oriented programming, each object having its own queue and random parameters.

By using it with a queue for each element of a 2D grid, you can achieve loops like this one:

Tutorials list Next tutorial